공간인접성

원문

자료실에도 올린 내용입니다.

글 중에 다음과 같은 부분이 눈길을 끕니다.

11) 공간의존성(spatial dependence)은 지리학의 제 1 법칙의 작용에 따른 것이므로 공간적으로 군집된 관찰을 결과로 보여줄 것이다. 공간의존성은 통계의 기본가정인 독립성과 상대적인 개념이다.

격자자료의 분석에서 중요한 것은 자료의 공간적 배열(위상 관계, 인접성)을 표현하고 어떤 통계적 검정이나 모델을 위해 시작점을 형성하는 공간가중치행렬(spatial weight mat rix )15)이다.

ESDA의 장점은 공간 상관성의 국지적인 패턴을 시각화하고, 국지적 불안정성을 확인하고 공간 이질성의 고립지역을 발견할 수 있다는 것이다(An selin , 1999). 공간통계분석에서 ESDA는 최근에 발달을 거듭하고 있고 매우 활동적인 연구 영역으로서 자연과학과 사회과학에서 과학적 자료분석의 핵심이 되고 있다.

15) 전통적인 생태학적 연구방법에서 무시되었던 이웃과의 관계를 정의하기 위해서 공간적 가중치 행렬(Spatial Weight s Matrices )의 개념은 매우 중요하다. 공간 가중치는 관찰들의 인접성이나 공간적 연계의 측정이다. 이것은 공간 이웃이나 공간 거리에 의한 값인 W(n×n)로 표시되는 행렬로 정의될 수 있다. 공간 가중치 행렬은 위치사이의 잠재적인 상호작용의 강도를 표현한다. 공간적인 배열 그 자체는 공간적 자기상관이나 공간적 상관관계에서 드러나는 공간적 상호작용에 대한 중요한 결정인자가 되는 것으로 고려되었다(Anselin, 1992). 부록1 참고.

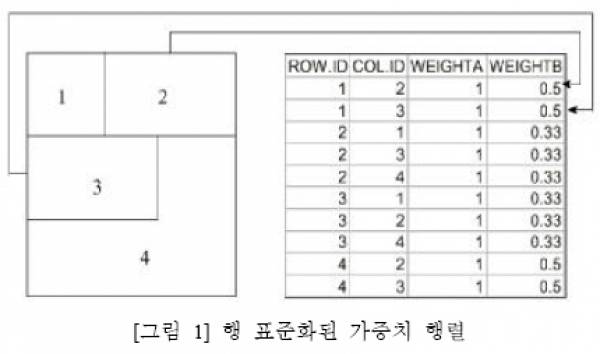
그림을 보면 행렬을 구성하는 단계가 나옵니다.

공간통계에서 면단위 분석을 실시할때는 위 그림과 같이 면들끼리와 위상관계가 중요합니다.(논문에 그렇게 나왔습니다.^^) 때문에 폴리곤끼리의 인접성이나 접근성을 위와 같은 형태로 만들어서 공간통계에 응용을 하네요… ^^

저는 주로 분석을 할 때는 폴리곤(셀이 됐든 블록이 됐던)단위로 점데이터들을 요약(합이나 평균 등)하여 그 요약정보만을 가지고 통계분석의 단위로 활용하였습니다. 제가 지금까지 놓친 것은 폴리곤별로 의미있는 통계 값만을 구했지 폴리곤들의 위상에는 신경을 쓰지 않았다는 것입니다. 그러니까 폴리곤들이 어떤놈하고 인접했는지에 대한 관심은 없었던 것이죠… 하지만 공간통계는 기본적으로 셀들간 인접성을 파악하고 어떤 지역이 서로간에 상관관계가 높은(공간적가기상관) 녀석들인지를 먼저 파악하는 작업을 선행합니다. 그리고 공간적자기상관이 높을 경우 이에대한 처리를 해주는 작업을 거쳐야합니다. (공간적 의존성은 변수간 상관관계를 높게 나타나게 하기 때문에 이를 통제하기 위한 방안으로 위와 같은 인접성을 파악합니다. ) GIS는 기본적으로 폴리곤이 만들어 지게 되면 폴리곤간 위상을 정립하는 기능이 있습니다. 위 그림과 같은 행렬처럼요…. 이제서야 왜 그러한 위상정립하는 기능이 있는지 이해가 가는군요.. 이거 재미있네요…이형민님께서 계속 정리를 해주실것으로 믿고… 저는 찾은 논문만 올립니다. 이거 스터디 만들어도 되겠는데요… ^^그때그때 궁금한거나 어설프지만 이해된게 있으면 이런 방식으로 꾸준히 올리고 잘 정리가 되는 시점이 오면 정리를 해보도록 하겠습니다. ^^

자세한 것은 다운로드 받아서 읽어 보세요… ^^

같이 공부해보고 싶어서 이렇게 올립니다.(아래는 간략 내용)

2 .3 범 죄 분 석 과 공 간 통 계 분 석 2 .3 . 1 공 간 통 계 분 석 공간자료의 통계적인 분석은 최근 주류 사회과학의 방법론으로 그 수용이 증가하고 있다. 일반적으로 자연과학 특히 토양학이나 수문학같은 분야와는 달리 사 회과학에서 공간 분석의 수용과 이용은 매우 최근의 일이다(Anselin, 2000). 이러한 현상은 공간통계분석, 특히 탐색적 공간자료분석(exploratory spatial data analysis , ESDA)의 대두 때문이라고 해도 과언이 아니다. ESDA는 공간자료의 공간 분포를 묘사하고 시각화하는 것, 불규칙적인 위치나 공간적인 이례지역(out lier s )을 확인하고, 공간 이질의 다른 형태와 공간적 체제를 제시하기 위한 기술들의 집합이다(Anselin, 1998). ESDA는 자료의 공간적 측면, 즉 공간적 의존성11)과 공간적 이질성12)에 초점을 둔다. 이것과 탐색적 자료분석 (Exploratory data analy sis , EDA )과의 차이점으로 ESDA는 공간자료의 특별한 본질인 공간적 자기상관(spatial aut ocorr elat ion )13)을 고려한다는 것이다. ESDA는 공간분석과 GIS기술과의 통합에 의해 더욱 발달되었고, 여러 학자들에 의해 두 영역의 통합에 관한 연구가 이루어지고 있다.(Goodchild, e t. al., 1992; Ans elin and Bao, 1997; Anselin, 1998).

11) 공간의존성(spatial dependence)은 지리학의 제 1 법칙의 작용에 따른 것이므로 공간적으로 군집된 관찰을 결과로 보여줄 것이다. 공간의존성은 통계의 기본가정 인 독립성과 상대적인 개념이다. 12) 공간이질성(spatial heterogeneity )는 본래 각각의 위치가 다르기 때문에 생기는 공간적 혹은 지역적 차이와 관련되는 것이다. 13) 공간적 자기상관(spatial autocorrelation)은 어떤 연구 지역의 하위 지역에 대한 변량 값의 분포가 주변 지역의 동일한 변량이 유사한 분포를 이루도록 영향을 미 칠 경우에 존재한다(유은혜, 1999; Cliif, A.D. and Ord, J .K., 1973, Spatial A utocorr elation, Pion, London.). 패턴의 존재와 부재는 공간적 자기상관의 개념 에 의해 나타난다. 즉, 어떤 지역에서 높은 값이 있을 때 이웃하는 주변지역에도 높은 값을 가지고 있고, 낮은 값을 가진 지역에 이웃하는 지역 역시 낮은 값을 가질 때 정적인 공간적 자기상관 또는 공간적 군집이 있다고 말한다. 그 반대는 음의 공간전 자기상관 혹은 공간적 이례지역이라고 한다.

공간적 자기상관은 사회과학과 자연과학에서 서로 다른 인식으로 개념화된다. 범죄분석과 같은 사회과학 연구에서는 보통 격자(lat tice )자료14)를 통해 공간적 자 기상관을 개념화한다. 격자자료의 분석에서 중요한 것은 자료의 공간적 배열(위상 관계, 인접성)을 표현하고 어떤 통계적 검정이나 모델을 위해 시작점을 형성하는 공간가중치행렬(spatial weight mat rix )15)이다.

공간적 자기상관은 전역적인 지표와 국지적인 지표로 구분할 수 있다. 일반적 으로 이용되는 전역적 자기상관 지표인 Mor an ' I와 Geary ' c는 자료에서 의존성의 전체적인 패턴을 하나의 지표로 요약한다. 그러나 GIS에서 전역적 자기상관지표의 단점은 공간상에서 일정한 평균과 분산을 요구하는 공간적 안정성의 가정에 기반하고 있다는 것이다. 이것은 보통 GIS에서 분석하는 자료의 양이 방대하다는 점을 고려했을 때 의미없는 결과나 잘못된 공간 상관성 분석을 도출할 수 있다. ESDA의 장점은 공간 상관성의 국지적인 패턴을 시각화하고, 국지적 불안정성을 확인하고 공간 이질성의 고립지역을 발견할 수 있다는 것이다(An selin , 1999). 공 간통계분석에서 ESDA는 최근에 발달을 거듭하고 있고 매우 활동적인 연구 영역으로서 자연과학과 사회과학에서 과학적 자료분석의 핵심이 되고 있다.

14) Cressie(1993)는 공간자료를 격자(lattice), 지리통계적(geostatistical), 점(point)의 세 가지로 분류하였다. 격자자료는 규칙적이거나 불규칙적인 면단위와 관련된 관찰이고, 지리통계적자료는 공간상에서 연속적인 변동과 관련된 관찰이다. 그리고 점패턴은 공간상의 위치에서 사건의 발생이다. 15) 전통적인 생태학적 연구방법에서 무시되었던 이웃과의 관계를 정의하기 위해서 공간적 가중치 행렬(Spatial Weight s Matrices )의 개념은 매우 중요하다. 공간 가중치는 관찰들의 인접성이나 공간적 연계의 측정이다. 이것은 공간 이웃이나 공간 거리에 의한 값인 W(n×n)로 표시되는 행렬로 정의될 수 있다. 공간 가중치 행렬은 위치사이의 잠재적인 상호작용의 강도를 표현한다. 공간적인 배열 그 자체는 공간적 자기상관이나 공간적 상관관계에서 드러나는 공간적 상호작용에 대한 중요한 결정인자가 되는 것으로 고려되었다(Anselin, 1992). 부록1 참고.